BCI Kickstarter #05 : Signal Processing in Python: Shaping EEG Data for BCI Applications
Welcome back to our BCI crash course! We've covered the fundamentals of BCIs, explored the brain's electrical activity, and equipped ourselves with the essential Python libraries for BCI development. Now, it's time to roll up our sleeves and dive into the practical world of signal processing. In this blog, we will transform raw EEG data into a format primed for BCI applications using MNE-Python. We will implement basic filters, create epochs around events, explore time-frequency representations, and learn techniques for removing artifacts. To make this a hands-on experience, we will work with the MNE sample dataset, a combined EEG and MEG recording from an auditory and visual experiment.
Getting Ready to Process: Load the Sample Dataset
First, let's load the sample dataset. If you haven't already, make sure you have MNE-Python installed (using conda install -c conda-forge mne). Then, run the following code:
import mne
# Load the sample dataset
data_path = mne.datasets.sample.data_path()
raw_fname = data_path + '/MEG/sample/sample_audvis_filt-0-40_raw.fif'
raw = mne.io.read_raw_fif(raw_fname, preload=True)
# Set the EEG reference to the average
raw.set_eeg_reference('average')
This code snippet loads the EEG data from the sample dataset into a raw object, ready for our signal processing adventures.
Implementing Basic Filters: Refining the EEG Signal
Raw EEG data is often contaminated by noise and artifacts from various sources, obscuring the true brain signals we're interested in. Filtering is a fundamental signal processing technique that allows us to selectively remove unwanted frequencies from our EEG signal.
Applying Filters with MNE: Sculpting the Frequency Landscape
MNE-Python provides a simple yet powerful interface for applying different types of filters to our EEG data using the raw.filter() function. Let's explore the most common filter types:
- High-Pass Filtering: Removes slow drifts and DC offsets, often caused by electrode movement or skin potentials. These low-frequency components can distort our analysis and make it difficult to identify event-related brain activity. Apply a high-pass filter with a cutoff frequency of 0.1 Hz to our sample data using:
raw_highpass = raw.copy().filter(l_freq=0.1, h_freq=None)
- Low-Pass Filtering: Removes high-frequency noise, which can originate from muscle activity or electrical interference. This noise can obscure the slower brain rhythms we're often interested in, such as alpha or beta waves. Apply a low-pass filter with a cutoff frequency of 30 Hz using:
raw_lowpass = raw.copy().filter(l_freq=None, h_freq=30)
- Band-Pass Filtering: Combines high-pass and low-pass filtering to isolate a specific frequency band. This is useful when we're interested in analyzing activity within a particular frequency range, such as the alpha band (8-12 Hz), which is associated with relaxed wakefulness. Apply a band-pass filter to isolate the alpha band using:
raw_bandpass = raw.copy().filter(l_freq=8, h_freq=12)
- Notch Filtering: Removes a narrow band of frequencies, typically used to eliminate power line noise (50/60 Hz) or other specific interference. This noise can create rhythmic artifacts in our data that can interfere with our analysis. Apply a notch filter at 50 Hz using:
raw_notch = raw.copy().notch_filter(freqs=50)
Visualizing Filtered Data: Observing the Effects
To see how filtering shapes our EEG signal, let's visualize the results using MNE-Python's plotting functions:
- Time-Domain Plots: Plot the raw and filtered EEG traces in the time domain using raw.plot(), raw_highpass.plot(), etc. Observe how the different filters affect the appearance of the signal.
- PSD Plots: Visualize the power spectral density (PSD) of the raw and filtered data using raw.plot_psd(), raw_highpass.plot_psd(), etc. Notice how filtering modifies the frequency content of the signal, attenuating power in the filtered bands.
Experiment and Explore: Shaping Your EEG Soundscape
Now it's your turn! Experiment with applying different filter settings to the sample dataset. Change the cutoff frequencies, try different filter types, and observe how the resulting EEG signal is transformed. This hands-on exploration will give you a better understanding of how filtering can be used to refine EEG data for BCI applications.
Epoching and Averaging: Extracting Event-Related Brain Activity
Filtering helps us refine the overall EEG signal, but for many BCI applications, we're interested in how the brain responds to specific events, such as the presentation of a stimulus or a user action. Epoching and averaging are powerful techniques that allow us to isolate and analyze event-related brain activity.
What are Epochs? Time-Locked Windows into Brain Activity
An epoch is a time-locked segment of EEG data centered around a specific event. By extracting epochs, we can focus our analysis on the brain's response to that event, effectively separating it from ongoing background activity.
Finding Events: Marking Moments of Interest
The sample dataset includes dedicated event markers, indicating the precise timing of each stimulus presentation and button press. We can extract these events using the mne.find_events() function:
events = mne.find_events(raw, stim_channel='STI 014')
This code snippet identifies the event markers from the STI 014 channel, commonly used for storing event information in EEG recordings.
Creating Epochs with MNE: Isolating Event-Related Activity
Now, let's create epochs around the events using the mne.Epochs() function:
# Define event IDs for the auditory stimuli
event_id = {'left/auditory': 1, 'right/auditory': 2}
# Set the epoch time window
tmin = -0.2 # 200 ms before the stimulus
tmax = 0.5 # 500 ms after the stimulus
# Create epochs
epochs = mne.Epochs(raw, events, event_id, tmin, tmax, baseline=(-0.2, 0))
This code creates epochs for the left and right auditory stimuli, spanning a time window from 200 ms before to 500 ms after each stimulus onset. The baseline argument applies baseline correction, subtracting the average activity during the pre-stimulus period (-200 ms to 0 ms) to remove any pre-existing bias.
Visualizing Epochs: Exploring Individual Responses
The epochs.plot() function allows us to explore individual epochs and visually inspect the data for artifacts:
epochs.plot()
This interactive visualization displays each epoch as a separate trace, allowing us to see how the EEG signal changes in response to the stimulus. We can scroll through epochs, zoom in on specific time windows, and identify any trials that contain excessive noise or artifacts.
Averaging Epochs: Revealing Event-Related Potentials
To reveal the consistent brain response to a specific event type, we can average the epochs for that event. This averaging process reduces random noise and highlights the event-related potential (ERP), a characteristic waveform reflecting the brain's processing of the event.
# Average the epochs for the left auditory stimulus
evoked_left = epochs['left/auditory'].average()
# Average the epochs for the right auditory stimulus
evoked_right = epochs['right/auditory'].average()
Plotting Evoked Responses: Visualizing the Average Brain Response
MNE-Python provides a convenient function for plotting the average evoked response:
evoked_left.plot()
evoked_right.plot()
This visualization displays the average ERP waveform for each auditory stimulus condition, showing how the brain's electrical activity changes over time in response to the sounds.
Analyze and Interpret: Unveiling the Brain's Auditory Processing
Now it's your turn! Analyze the evoked responses for the left and right auditory stimuli. Compare the waveforms, looking for differences in amplitude, latency, or morphology. Can you identify any characteristic ERP components, such as the N100 or P300? What do these differences tell you about how the brain processes sounds from different spatial locations?
Time-Frequency Analysis: Unveiling Dynamic Brain Rhythms
Epoching and averaging allow us to analyze the brain's response to events in the time domain. However, EEG signals are often non-stationary, meaning their frequency content changes over time. To capture these dynamic shifts in brain activity, we turn to time-frequency analysis.
Time-frequency analysis provides a powerful lens for understanding how brain rhythms evolve in response to events or cognitive tasks. It allows us to see not just when brain activity changes but also how the frequency content of the signal shifts over time.
Wavelet Transform with MNE: A Window into Time and Frequency
The wavelet transform is a versatile technique for time-frequency analysis. It decomposes the EEG signal into a set of wavelets, functions that vary in both frequency and time duration, providing a detailed representation of how different frequencies contribute to the signal over time.
MNE-Python offers the mne.time_frequency.tfr_morlet() function for computing the wavelet transform:
from mne.time_frequency import tfr_morlet
# Define the frequencies of interest
freqs = np.arange(7, 30, 1) # From 7 Hz to 30 Hz in 1 Hz steps
# Set the number of cycles for the wavelets
n_cycles = freqs / 2. # Increase the number of cycles with frequency
# Compute the wavelet transform for the left auditory epochs
power_left, itc_left = tfr_morlet(epochs['left/auditory'], freqs=freqs, n_cycles=n_cycles, use_fft=True, return_itc=True)
# Compute the wavelet transform for the right auditory epochs
power_right, itc_right = tfr_morlet(epochs['right/auditory'], freqs=freqs, n_cycles=n_cycles, use_fft=True, return_itc=True)
This code computes the wavelet transform for the left and right auditory epochs, focusing on frequencies from 7 Hz to 30 Hz. The n_cycles parameter determines the time resolution and frequency smoothing of the transform.
Visualizing Time-Frequency Representations: Spectrograms of Brain Activity
To visualize the time-frequency representations, we can use the mne.time_frequency.AverageTFR.plot() function:
power_left.plot([0], baseline=(-0.2, 0), mode='logratio', title="Left Auditory Stimulus")
power_right.plot([0], baseline=(-0.2, 0), mode='logratio', title="Right Auditory Stimulus")
This code displays spectrograms, plots that show the power distribution across frequencies over time. The baseline argument normalizes the power values to the pre-stimulus period, highlighting event-related changes.
Interpreting Time-Frequency Results
Time-frequency representations reveal how the brain's rhythmic activity evolves over time. Increased power in specific frequency bands after the stimulus can indicate the engagement of different cognitive processes. For example, we might observe increased alpha power during sensory processing or enhanced beta power during attentional engagement.
Discovering Dynamic Brain Patterns
Now, explore the time-frequency representations for the left and right auditory stimuli. Look for changes in power across different frequency bands following the stimulus onset. Do you observe any differences between the two conditions? What insights can you gain about the dynamic nature of auditory processing in the brain?
Artifact Removal Techniques: Cleaning Up Noisy Data
Even after careful preprocessing, EEG data can still contain artifacts that distort our analysis and hinder BCI performance. This section explores techniques for identifying and removing these unwanted signals, ensuring cleaner and more reliable data for our BCI applications.
Identifying Artifacts: Spotting the Unwanted Guests
- Visual Inspection: We can visually inspect raw EEG traces (raw.plot()) and epochs (epochs.plot()) to identify obvious artifacts, such as eye blinks, muscle activity, or electrode movement.
- Automated Methods: Algorithms can automatically detect specific artifact patterns based on their characteristic features, such as the high amplitude and slow frequency of eye blinks.
Rejecting Noisy Epochs: Discarding the Troublemakers
One approach to artifact removal is to simply discard noisy epochs. We can set rejection thresholds based on signal amplitude using the reject parameter in the mne.Epochs() function:
# Set rejection thresholds for EEG and EOG channels
reject = dict(eeg=150e-6) # Reject epochs with EEG activity exceeding 150 µV
# Create epochs with rejection criteria
epochs = mne.Epochs(raw, events, event_id, tmin, tmax, baseline=(-0.2, 0), reject=reject)
This code rejects epochs where the peak-to-peak amplitude of the EEG signal exceeds 150 µV, helping to eliminate trials contaminated by high-amplitude artifacts.
Independent Component Analysis (ICA): Unmixing the Signal Cocktail
Independent component analysis (ICA) is a powerful technique for separating independent sources of activity within EEG data. It assumes that the recorded EEG signal is a mixture of independent signals originating from different brain regions and artifact sources.
MNE-Python provides the mne.preprocessing.ICA() function for performing ICA:
from mne.preprocessing import ICA
# Create an ICA object
ica = ICA(n_components=20, random_state=97)
# Fit the ICA to the EEG data
ica.fit(raw)
We can then visualize the independent components using ica.plot_components() and identify components that correspond to artifacts based on their characteristic time courses and scalp topographies. Once identified, these artifact components can be removed from the data, leaving behind cleaner EEG signals.
Experiment and Explore: Finding the Right Cleaning Strategy
Artifact removal is an art as much as a science. Experiment with different artifact removal techniques and settings to find the best strategy for your specific dataset and BCI application. Visual inspection, rejection thresholds, and ICA can be combined to achieve optimal results.
Mastering the Art of Signal Processing
We've journeyed through the essential steps of signal processing in Python, transforming raw EEG data into a form ready for BCI applications. We've implemented basic filters, extracted epochs, explored time-frequency representations, and tackled artifact removal, building a powerful toolkit for shaping and refining brainwave data.
Remember, careful signal processing is the foundation for reliable and accurate BCI development. By mastering these techniques, you're well on your way to creating innovative applications that translate brain activity into action.
Resources and Further Reading
- MIT course on Signals and Systems: https://ocw.mit.edu/courses/res-6-007-signals-and-systems-spring-2011/
- Book: Smith, S. W. (2002). The scientist and engineer's guide to digital signal processing. California Technical Publishing.
From Processed Signals to Intelligent Algorithms: The Next Level
This concludes our deep dive into signal processing techniques using Python and MNE-Python. You've gained valuable hands-on experience in cleaning up, analyzing, and extracting meaningful information from EEG data, setting the stage for the next exciting phase of our BCI journey.
In the next post, we'll explore the world of machine learning for BCI, where we'll train algorithms to decode user intent, predict mental states, and control external devices directly from brain signals. Get ready to witness the magic of intelligent algorithms transforming processed brainwaves into real-world BCI applications!
In our previous blog, we explored how biosignals serve as the body's internal language—electrical, mechanical, and chemical messages that allow us to understand and interface with our physiology. Among these, electrical biosignals are particularly important for understanding how our nervous system, muscles, and heart function in real time. In this article, we’ll take a closer look at three of the most widely used electrical biosignals—EEG, ECG, and EMG—and their growing role in neurotechnology, diagnostics, performance tracking, and human-computer interaction. If you're new to the concept of biosignals, you might want to check out our introductory blog for a foundational overview.
"The body is a machine, and we must understand its currents if we are to understand its functions."-Émil du Bois-Reymond, pioneer in electrophysiology.
Life, though rare in the universe, leaves behind unmistakable footprints—biosignals. These signals not only confirm the presence of life but also narrate what a living being is doing, feeling, or thinking. As technology advances, we are learning to listen to these whispers of biology. Whether it’s improving health, enhancing performance, or building Brain-Computer Interfaces (BCIs), understanding biosignals is key.
Among the most studied biosignals are:
- Electroencephalogram (EEG) – from the brain
- Electrocardiogram (ECG) – from the heart
- Electromyogram (EMG) – from muscles
- Galvanic Skin Response (GSR) – from skin conductance
These signals are foundational for biosignal processing, real-time monitoring, and interfacing the human body with machines. In this article we look at some of these biosignals and some fascinating stories behind them.
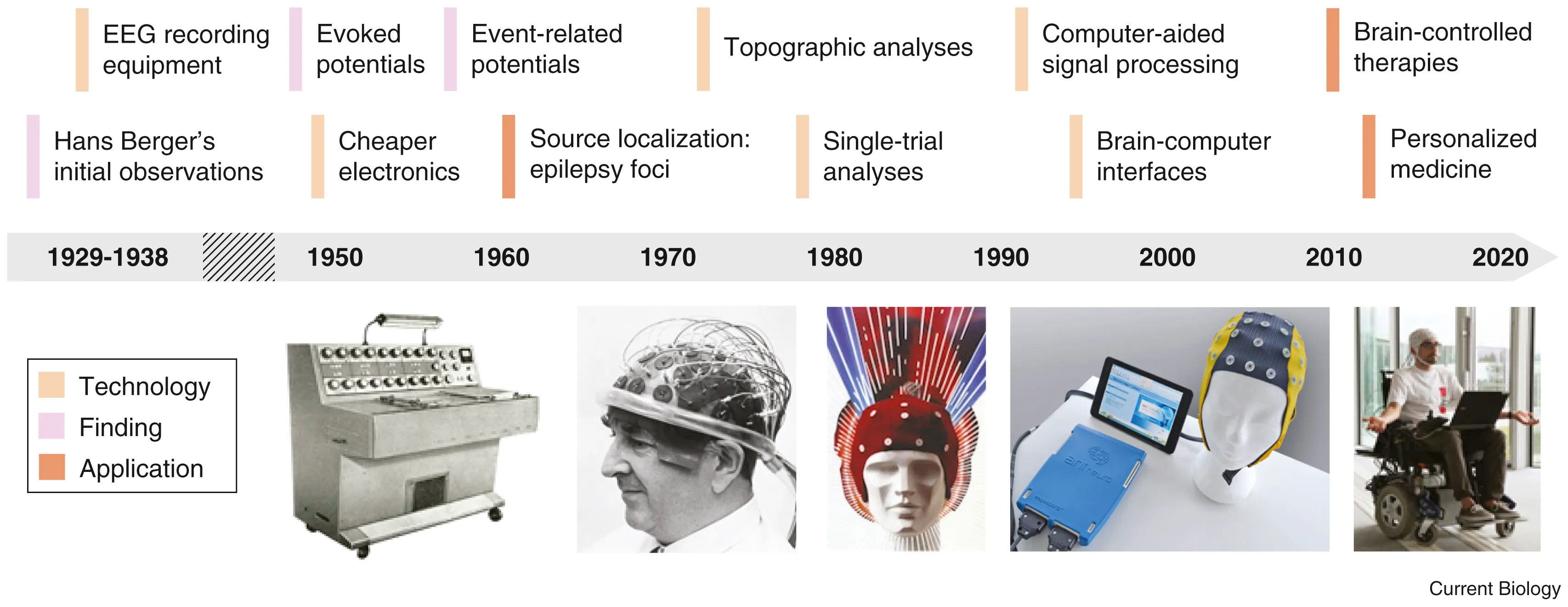
Electroencephalography (EEG): Listening to Brainwaves
In 1893, a 19 year old Hans Berger fell from a horse and had a near death experience. Little did he know that it would be a pivotal moment in the history of neurotechnology. The same day he received a telegram from his sister who was extremely concerned for him because she had a bad feeling. Hans Berger was convinced that this was due to the phenomenon of telepathy. After all, it was the age of radio waves, so why can’t there be “brain waves”? In his ensuing 30 year career telepathy was not established but in his pursuit, Berger became the first person to record brain waves.
When neurons fire together, they generate tiny electrical currents. These can be recorded using electrodes placed on the scalp (EEG), inside the skull (intracranial EEG), or directly on the brain (ElectroCorticogram). EEG signal processing is used not only to understand the brain’s rhythms but also in EEG-based BCI systems, allowing communication and control for people with paralysis. Event-Related Potentials (ERPs) and Local Field Potentials (LFPs) are specialized types of EEG signals that provide insights into how the brain responds to specific stimuli.
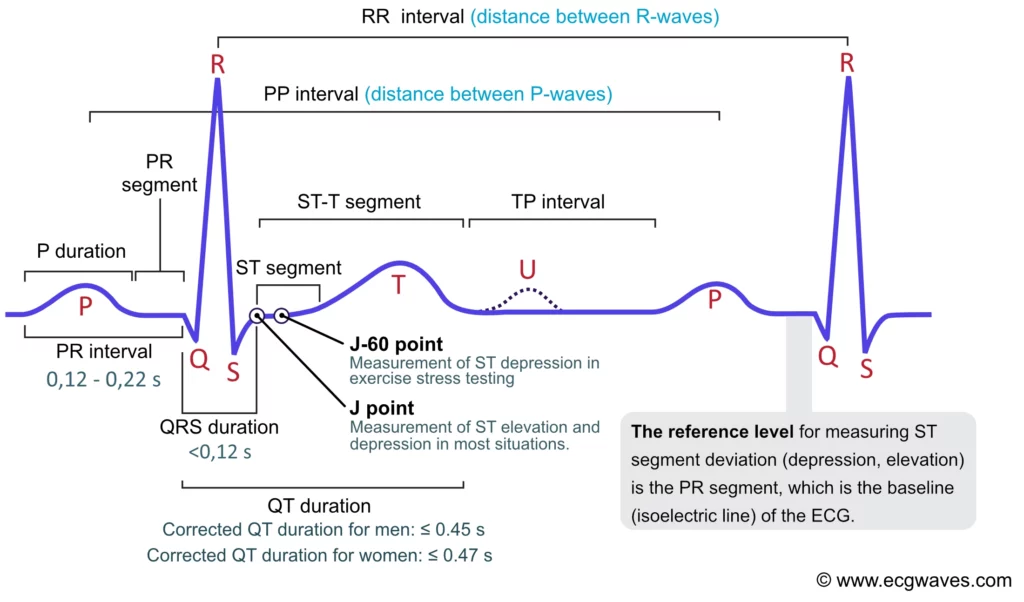
Electrocardiogram (ECG): The Rhythm of the Heart
The heart has its own internal clock which produces tiny electrical signals every time it beats. Each heartbeat starts with a small electrical impulse made by a special part of the heart called the sinoatrial (SA) node. This impulse spreads through the heart muscle and makes it contract, first the upper (atria) and then lower chambers (ventricles) – that’s what pumps blood. This process produces voltage changes, which can be recorded via electrodes on the skin.
This gives rise to the classic PQRST waveform, with each component representing a specific part of the heart’s cycle. Modern wearables and medical devices use ECG signal analysis to monitor heart health in real time.
Fun fact: The waveform starts with “P” because Willem Einthoven left room for earlier letters—just in case future scientists discovered pre-P waves! So, thanks to a cautious scientist, we have the quirky naming system we still follow today.
Electromyography (EMG): The Language of Movement
When we perform any kind of movement - lifting our arm, kicking our leg, smiling, blinking or even breathing- our brain sends electrical signals to our muscles telling them to contract. When these neurons, known as motor neurons fire they release electrical impulses that travel to the muscle, causing it to contract. This electrical impulse—called a motor unit action potential (MUAP)—is what we see as an EMG signal. So, every time we move, we are generating an EMG signal!
Medical Applications
Medically, EMG is used for monitoring muscle fatigue especially in rehabilitation settings and muscle recovery post-injury or surgery. This helps clinicians measure progress and optimize therapy. EMG can distinguish between voluntary and involuntary movements, making it useful in diagnosing neuromuscular disorders, assessing stroke recovery, spinal cord injuries, and motor control dysfunctions.
Performance and Sports Science
In sports science, EMG can tell us muscle-activation timing and quantify force output of muscle groups. These are important factors to measure performance improvement in any sport. The number of motor units recruited and the synergy between muscle groups, helps us capture “mind-muscle connection” and muscle memory. Such things which were previously spoken off in a figurative manner can be scientifically measured and quantified using EMG. By tracking these parameters we get a window into movement efficiency and athletic performance. EMG is also used for biofeedback training, enabling individuals to consciously correct poor movement habits or retrain specific muscles
Beyond medicine and sports, EMG is used for gesture recognition in AR/VR and gaming, silent speech detection via facial EMG, and next-gen prosthetics and wearable exosuits that respond to the user’s muscle signals. EMG can be used in brain-computer interfaces (BCIs), helping paralyzed individuals control digital devices or communicate through subtle muscle activity. EMG bridges the gap between physiology, behavior, and technology—making it a critical tool in healthcare, performance optimization, and human-machine interaction.
As biosignal processing becomes more refined and neurotech devices more accessible, we are moving toward a world where our body speaks—and machines understand. Whether it’s detecting the subtlest brainwaves, tracking a racing heart, or interpreting muscle commands, biosignals are becoming the foundation of the next digital revolution. One where technology doesn’t just respond, but understands.
The human body is constantly generating data—electrical impulses, chemical fluctuations, and mechanical movements—that provide deep insights into our bodily functions, and cognitive states. These measurable physiological signals, known as biosignals, serve as the body's natural language, allowing us to interpret and interact with its inner workings. From monitoring brain activity to assessing muscle movement, biosignals are fundamental to understanding human physiology and expanding the frontiers of human-machine interaction. But what exactly are biosignals? How are they classified, and why do they matter? In this blog, we will explore the different types of biosignals, the science behind their measurement, and the role they play in shaping the future of human health and technology.
What are Biosignals?
Biosignals refer to any measurable signal originating from a biological system. These signals are captured and analyzed to provide meaningful information about the body's functions. Traditionally used in medicine for diagnosis and monitoring, biosignals are now at the forefront of research in neurotechnology, wearable health devices, and human augmentation.
The Evolution of Biosignal Analysis
For centuries, physicians have relied on pulse measurements to assess a person’s health. In ancient Chinese and Ayurvedic medicine, the rhythm, strength, and quality of the pulse were considered indicators of overall well-being. These early methods, while rudimentary, laid the foundation for modern biosignal monitoring.
Today, advancements in sensor technology, artificial intelligence, and data analytics have transformed biosignal analysis. Wearable devices can continuously track heart rate, brain activity, and oxygen levels with high precision. AI-driven algorithms can detect abnormalities in EEG or ECG signals, helping diagnose neurological and cardiac conditions faster than ever. Real-time biosignal monitoring is now integrated into medical, fitness, and neurotechnology applications, unlocking insights that were once beyond our reach.
This leap from manual pulse assessments to AI-powered biosensing is reshaping how we understand and interact with our own biology.
Types of Biosignals:-
Biosignals come in three main types
- Electrical Signals: Electrical signals are generated by neural and muscular activity, forming the foundation of many biosignal applications. Electroencephalography (EEG) captures brain activity, playing a crucial role in understanding cognition and diagnosing neurological disorders. Electromyography (EMG) measures muscle activity, aiding in rehabilitation and prosthetic control. Electrocardiography (ECG) records heart activity, making it indispensable for cardiovascular monitoring. Electrooculography (EOG) tracks eye movements, often used in vision research and fatigue detection.
- Mechanical Signals: Mechanical signals arise from bodily movements and structural changes, providing valuable physiological insights. Respiration rate tracks breathing patterns, essential for sleep studies and respiratory health. Blood pressure serves as a key indicator of cardiovascular health and stress responses. Muscle contractions help in analyzing movement disorders and biomechanics, enabling advancements in fields like sports science and physical therapy.
- Chemical Signals: Chemical signals reflect the biochemical activity within the body, offering a deeper understanding of physiological states. Neurotransmitters like dopamine and serotonin play a critical role in mood regulation and cognitive function. Hormone levels serve as indicators of stress, metabolism, and endocrine health. Blood oxygen levels are vital for assessing lung function and metabolic efficiency, frequently monitored in medical and athletic settings.
How Are Biosignals Measured?
After understanding what biosignals are and their different types, the next step is to explore how these signals are captured and analyzed. Measuring biosignals requires specialized sensors that detect physiological activity and convert it into interpretable data. This process involves signal acquisition, processing, and interpretation, enabling real-time monitoring and long-term health assessments.
- Electrodes & Wearable Sensors
Electrodes measure electrical biosignals like EEG (brain activity), ECG (heart activity), and EMG (muscle movement) by detecting small voltage changes. Wearable sensors, such as smartwatches, integrate these electrodes for continuous, non-invasive monitoring, making real-time health tracking widely accessible.
- Optical Sensors
Optical sensors, like pulse oximeters, use light absorption to measure blood oxygen levels (SpO₂) and assess cardiovascular and respiratory function. They are widely used in fitness tracking, sleep studies, and medical diagnostics.
- Pressure Sensors
These sensors measure mechanical biosignals such as blood pressure, respiratory rate, and muscle contractions by detecting force or air pressure changes. Blood pressure cuffs and smart textiles with micro-pressure sensors provide valuable real-time health data.
- Biochemical Assays
Biochemical sensors detect chemical biosignals like hormones, neurotransmitters, and metabolic markers. Advanced non-invasive biosensors can now analyze sweat composition, hydration levels, and electrolyte imbalances without requiring a blood sample.
- Advanced AI & Machine Learning in Biosignal Analysis
Artificial intelligence (AI) and machine learning (ML) have transformed biosignal interpretation by enhancing accuracy and efficiency. These technologies can detect abnormalities in EEG, ECG, and EMG signals, helping with early disease diagnosis. They also filter out noise and artifacts, improving signal clarity for more precise analysis. By analyzing long-term biosignal trends, AI can predict potential health risks and enable proactive interventions. Additionally, real-time AI-driven feedback is revolutionizing applications like neurofeedback and biofeedback therapy, allowing for more personalized and adaptive healthcare solutions. The integration of AI with biosignal measurement is paving the way for smarter diagnostics, personalized medicine, and enhanced human performance tracking.
Figure : The image provides an overview of biosignals detectable from different parts of the human body and their corresponding wearable sensors. It categorizes biosignals such as EEG, ECG, and EMG, demonstrating how wearable technologies enable real-time health monitoring and improve diagnostic capabilities.
The Future of Biosignals
As sensor technology and artificial intelligence continue to evolve, biosignals will become even more integrated into daily life, shifting from reactive healthcare to proactive and predictive wellness solutions. Advances in non-invasive monitoring will allow for continuous tracking of vital biomarkers, reducing the need for clinical testing. Wearable biosensors will provide real-time insights into hydration, stress, and metabolic health, enabling individuals to make data-driven decisions about their well-being. Artificial intelligence will play a pivotal role in analyzing complex biosignal patterns, enabling early detection of diseases before symptoms arise and personalizing treatments based on an individual's physiological data.
The intersection of biosignals and brain-computer interfaces (BCIs) is also pushing the boundaries of human-machine interaction. EEG-based BCIs are already enabling users to control digital interfaces with their thoughts, and future developments could lead to seamless integration between the brain and external devices. Beyond healthcare, biosignals will drive innovations in adaptive learning, biometric authentication, and even entertainment, where music, lighting, and virtual experiences could respond to real-time physiological states. As these technologies advance, biosignals will not only help us understand the body better but also enhance human capabilities, bridging the gap between biology and technology in unprecedented ways.
Welcome back to our BCI crash course! Over the past eight blogs, we have explored the fascinating intersection of neuroscience, engineering, and machine learning, from the fundamental concepts of BCIs to the practical implementation of real-world applications. In this final installment, we will shift our focus to the future of BCI, delving into advanced topics and research directions that are pushing the boundaries of mind-controlled technology. Get ready to explore the exciting possibilities of hybrid BCIs, adaptive algorithms, ethical considerations, and the transformative potential that lies ahead for this groundbreaking field.
Hybrid BCIs: Combining Paradigms for Enhanced Performance
As we've explored in previous posts, different BCI paradigms leverage distinct brain signals and have their strengths and limitations. Motor imagery BCIs excel at decoding movement intentions, P300 spellers enable communication through attention-based selections, and SSVEP BCIs offer high-speed control using visual stimuli.
What are Hybrid BCIs? Synergy of Brain Signals
Hybrid BCIs combine multiple BCI paradigms, integrating different brain signals to create more robust, versatile, and user-friendly systems. Imagine a BCI that leverages both motor imagery and SSVEP to control a robotic arm with greater precision and flexibility, or a system that combines P300 with error-related potentials (ErrPs) to improve the accuracy and speed of a speller.
Benefits of Hybrid BCIs: Unlocking New Possibilities
Hybrid BCIs offer several advantages over single-paradigm systems:
- Improved Accuracy and Reliability: Combining complementary brain signals can enhance the signal-to-noise ratio and reduce the impact of individual variations in brain activity, leading to more accurate and reliable BCI control.
- Increased Flexibility and Adaptability: Hybrid BCIs can adapt to different user needs, tasks, and environments by dynamically switching between paradigms or combining them in a way that optimizes performance.
- Richer and More Natural Interactions: Integrating multiple BCI paradigms opens up possibilities for creating more intuitive and natural BCI interactions, allowing users to control devices with a greater range of mental commands.
Examples of Hybrid BCIs: Innovations in Action
Research is exploring various hybrid BCI approaches:
- Motor Imagery + SSVEP: Combining motor imagery with SSVEP can enhance the control of robotic arms. Motor imagery provides continuous control signals for movement direction, while SSVEP enables discrete selections for grasping or releasing objects.
- P300 + ErrP: Integrating P300 with ErrPs, brain signals that occur when we make errors, can improve speller accuracy. The P300 is used to select letters, while ErrPs can be used to automatically correct errors, reducing the need for manual backspacing.
Adaptive BCIs: Learning and Evolving with the User
One of the biggest challenges in BCI development is the inherent variability in brain signals. A BCI system that works perfectly for one user might perform poorly for another, and even a single user's brain activity can change over time due to factors like learning, fatigue, or changes in attention. This is where adaptive BCIs come into play, offering a dynamic and personalized approach to brain-computer interaction.
The Need for Adaptation: Embracing the Brain's Dynamic Nature
BCI systems need to adapt to several factors:
- Changes in User Brain Activity: Brain signals are not static. They evolve as users learn to control the BCI, become fatigued, or shift their attention. An adaptive BCI can track these changes and adjust its processing accordingly.
- Variations in Signal Quality and Noise: EEG recordings can be affected by various sources of noise, from muscle artifacts to environmental interference. An adaptive BCI can adjust its filtering and artifact rejection parameters to maintain optimal signal quality.
- Different User Preferences and Skill Levels: BCI users have different preferences for control strategies, feedback modalities, and interaction speeds. An adaptive BCI can personalize its settings to match each user's individual needs and skill level.
Methods for Adaptation: Tailoring BCIs to the Individual
Various techniques can be employed to create adaptive BCIs:
- Machine Learning Adaptation: Machine learning algorithms, such as those used for classification, can be trained to continuously learn and update the BCI model based on the user's brain data. This allows the BCI to adapt to changes in brain patterns over time and improve its accuracy and responsiveness.
- User Feedback Adaptation: BCIs can incorporate user feedback, either explicitly (through direct input) or implicitly (by monitoring performance and user behavior), to adjust parameters and optimize the interaction. For example, if a user consistently struggles to control a motor imagery BCI, the system could adjust the classification thresholds or provide more frequent feedback to assist them.
Benefits of Adaptive BCIs: A Personalized and Evolving Experience
Adaptive BCIs offer significant advantages:
- Enhanced Usability and User Experience: By adapting to individual needs and preferences, adaptive BCIs can become more intuitive and easier to use, reducing user frustration and improving the overall experience.
- Improved Long-Term Performance and Reliability: Adaptive BCIs can maintain high levels of performance and reliability over time by adjusting to changes in brain activity and signal quality.
- Personalized BCIs: Adaptive algorithms can tailor the BCI to each user's unique brain patterns, preferences, and abilities, creating a truly personalized experience.
Ethical Considerations: Navigating the Responsible Development of BCI
As BCI technology advances, it's crucial to consider the ethical implications of its development and use. BCIs have the potential to profoundly impact individuals and society, raising questions about privacy, autonomy, fairness, and responsibility.
Introduction: Ethics at the Forefront of BCI Innovation
Ethical considerations should be woven into the fabric of BCI research and development, guiding our decisions and ensuring that this powerful technology is used for good.
Key Ethical Concerns: Navigating a Complex Landscape
- Privacy and Data Security: BCIs collect sensitive brain data, raising concerns about privacy violations and potential misuse. Robust data security measures and clear ethical guidelines are crucial for protecting user privacy and ensuring responsible data handling.
- Agency and Autonomy: BCIs have the potential to influence user thoughts, emotions, and actions. It's essential to ensure that BCI use respects user autonomy and agency, avoiding coercion, manipulation, or unintended consequences.
- Bias and Fairness: BCI algorithms can inherit biases from the data they are trained on, potentially leading to unfair or discriminatory outcomes. Addressing these biases and developing fair and equitable BCI systems is essential for responsible innovation.
- Safety and Responsibility: As BCIs become more sophisticated and integrated into critical applications like healthcare and transportation, ensuring their safety and reliability is paramount. Clear lines of responsibility and accountability need to be established to mitigate potential risks and ensure ethical use.
Guidelines and Principles: A Framework for Responsible BCI
Efforts are underway to establish ethical guidelines and principles for BCI research and development. These guidelines aim to promote responsible innovation, protect user rights, and ensure that BCI technology benefits society as a whole.
Current Challenges and Future Prospects: The Road Ahead for BCI
While BCI technology has made remarkable progress, several challenges remain to be addressed before it can fully realize its transformative potential. However, the future of BCI is bright, with exciting possibilities on the horizon for enhancing human capabilities, restoring lost function, and improving lives.
Technical Challenges: Overcoming Roadblocks to Progress
- Signal Quality and Noise: Non-invasive BCIs, particularly those based on EEG, often suffer from low signal-to-noise ratios. Improving signal quality through advanced electrode designs, noise reduction algorithms, and a better understanding of brain signals is crucial for enhancing BCI accuracy and reliability.
- Robustness and Generalizability: Current BCI systems often work well in controlled laboratory settings but struggle to perform consistently across different users, environments, and tasks. Developing more robust and generalizable BCIs is essential for wider adoption and real-world applications.
- Long-Term Stability: Maintaining the long-term stability and performance of BCI systems, especially for implanted devices, is a significant challenge. Addressing issues like biocompatibility, signal degradation, and device longevity is crucial for ensuring the viability of invasive BCIs.
Future Directions: Expanding the BCI Horizon
- Non-invasive Advancements: Research is focusing on developing more sophisticated and user-friendly non-invasive BCI systems. Advancements in EEG technology, including dry electrodes, high-density arrays, and mobile brain imaging, hold promise for creating more portable, comfortable, and accurate non-invasive BCIs.
- Clinical Applications: BCIs are showing increasing promise for clinical applications, such as restoring lost motor function in individuals with paralysis, assisting in stroke rehabilitation, and treating neurological disorders like epilepsy and Parkinson's disease. Ongoing research and clinical trials are paving the way for wider adoption of BCIs in healthcare.
- Cognitive Enhancement: BCIs have the potential to enhance cognitive abilities, such as memory, attention, and learning. Research is exploring ways to use BCIs for cognitive training and to develop brain-computer interfaces that can augment human cognitive function.
- Brain-to-Brain Communication: One of the most futuristic and intriguing directions in BCI research is the possibility of direct brain-to-brain communication. Studies have already demonstrated the feasibility of transmitting simple signals between brains, opening up possibilities for collaborative problem-solving, enhanced empathy, and new forms of communication.
Resources for Further Learning and Development
- Brain-Computer Interface Wiki
- Research Journals and Conferences:some text
- Journal of Neural Engineering: https://iopscience.iop.org/journal/1741-2560 - A leading journal for BCI research and related fields.
- Brain-Computer Interfaces: https://www.tandfonline.com/toc/tbci20/current - A dedicated journal focusing on advances in BCI technology and applications.
Embracing the Transformative Power of BCI
From hybrid systems to adaptive algorithms, ethical considerations, and the exciting possibilities of the future, we've explored the cutting edge of BCI technology. This field is rapidly evolving, driven by advancements in neuroscience, engineering, and machine learning.
BCIs hold immense potential to revolutionize how we interact with technology, enhance human capabilities, restore lost function, and improve lives. As we continue to push the boundaries of mind-controlled technology, the future promises a world where our thoughts can seamlessly translate into actions, unlocking new possibilities for communication, control, and human potential.
As we wrap up this course with this final blog article, we hope that you gained an overview as well as practical expertise in the field of BCIs. Please feel free to reach out to us with feedback and areas of improvement. Thank you for reading along so far, and best wishes for further endeavors in your BCI journey!
